Solved 4. (Nonlinear Pendulum and elliptic integrals) The | Chegg.com
Solved tp = 4, (b) The correct formula from part (a) can be | Chegg.com
International Journal of Applied Mathematics ————————————————————– Volume 30 No. 3 201
Solved 5. Consider a simple pendulum of length 1 with a mass | Chegg.com
Pochhammer symbol 5.Hypergeometric Functions Hypergeometric equation ( Gauss' ODE & functions ) Regular singularities at Solution : Hypergeometric function. - ppt download
Solved The period of a simple pendulum is determined by the | Chegg.com
![Exact Solution of the Nonlinear Pendulum [No Approximations, engis gtfo] - YouTube](https://i.ytimg.com/vi/efvT2iUSjaA/maxresdefault.jpg "Exact Solution of the Nonlinear Pendulum [No Approximations, engis gtfo] - YouTube")
Exact Solution of the Nonlinear Pendulum [No Approximations, engis gtfo] - YouTube
Solved Problem 4 (5 points) The period of a simple pendulum | Chegg.com
SOLVED: Use the first five terms of the Maclaurin (Taylor series centered at zero) for the elliptic integral E(k) to estimate the period T of a I-mcter pendulum released at an angle
Elliptic integrals - CodeProject
How to Evaluate Complete Elliptic Integrals: 7 Steps - wikiHow Life
Elliptic Integral png images | PNGWing
Elliptic integrals - CodeProject
Kinds of elliptic integrals
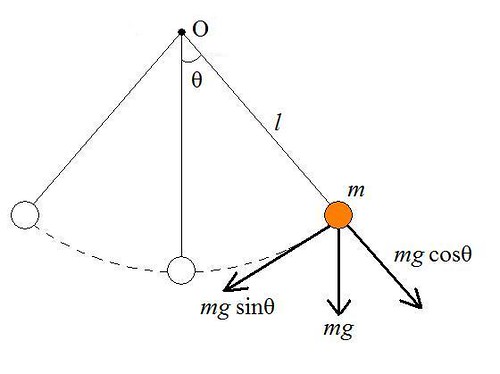
Elliptic Integrals Section 4.4 & Appendix B Brief math interlude: –Solutions to certain types of nonlinear oscillator problems, while not expressible. - ppt download
Pendulum (mechanics) - Wikipedia
Torque and Simple Harmonic Motion Week 13D2 Today's Reading Assignment Young and Freedman: ppt download
Topic 2: The pendulum
Elliptic integrals - CodeProject
Application Center - Maplesoft
Elliptic integrals - CodeProject
PDF) COMPLETE ANALYSIS OF THE NONLINEAR PENDULUM FOR AMPLITUDES IN ALL REGIMES USING NUMERICAL INTEGRATION | Youssef Mohammed - Academia.edu
MM61: Simple pendulum and elliptic integrals - YouTube
Answered: mass m is fixed to Pendulum A simple… | bartleby
Elliptic integral - Wikipedia
SOLVED: Determine the period of oscillations of the simple pendulum as function of the amplitude of oscillations D to be T = To 2K sin 2 (16) where de K(k) = (17)
![A treatise on gyrostatics and rotational motion . Thus for the quarter period of the pendulum vibrating over a finite arc, we have [ 12,XV, below] //i ( /] o2 ^ r-*r(|) (](https://c8.alamy.com/comp/2AKXFY4/a-treatise-on-gyrostatics-and-rotational-motion-thus-for-the-quarter-period-of-the-pendulum-vibrating-over-a-finite-arc-we-have-12xv-below-i-o2-r-r-lfflwgld-with-2=sin20o=cb2-where-cb-is-the-diameter-of-the-smaller-circle-in-fig-64-00-8-landeris-transformation-an-elliptic-integral-expressed-as-a-con-tinued-product-an-elliptic-integral-of-the-first-kind-can-be-transformed-into-anotherof-a-larger-modulus-and-a-smaller-amplitude-or-of-a-smaller-modulus-and-a-larger-ampli-tude-the-transformation-is-that-given-by-landen-phil-trim-1775-taking-th-2AKXFY4.jpg "A treatise on gyrostatics and rotational motion . Thus for the quarter period of the pendulum vibrating over a finite arc, we have [ 12,XV, below] //i ( /] o2 ^ r-*r(|) (")
A treatise on gyrostatics and rotational motion . Thus for the quarter period of the pendulum vibrating over a finite arc, we have [ 12,XV, below] //i ( /] o2 ^ r-*r(|) (
Solved Simple Pendulum In Section 4.8, we discussed the | Chegg.com
The "Simple" Pendulum
